Markov Chains
Basics

A stochastic model in some sense is a model which depends on some random process.

A Markov process named after Andrey Markov, is a stochastic process that satisfies the Markov property. Markov property is also refered to as "memorylessness". In probability theory and statistics, memorylessness is a property in which the next state is dependent on present state only.

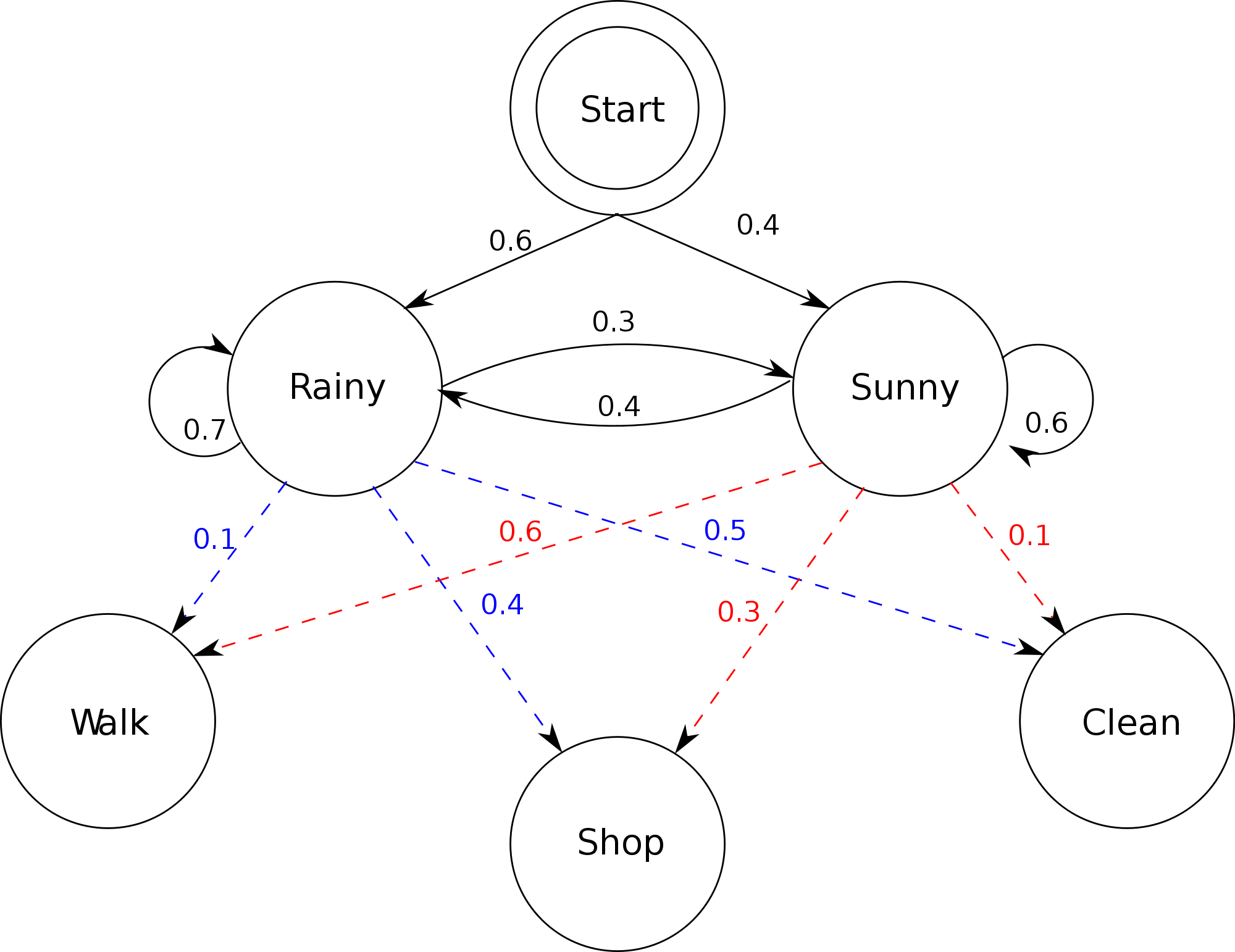
Markov chains have multitude of applications in real world including, study of cruise control systems, Ant colony optimization, Share price movement analysis, etc.

So as we can see, there are multiple ways in which we can use Markov chains to analyze or simulate real world processes.

Markov chain is a chain and is a type of Markov process with finite or countable state space. The changes of state in a Markov chain are called transition and the probability associated with those transition are known as transition probabilities. We can express a Markov chain with the use of transition matrix with describing the probability in the transition.

Transition Matrix (Stochastic Matrix)

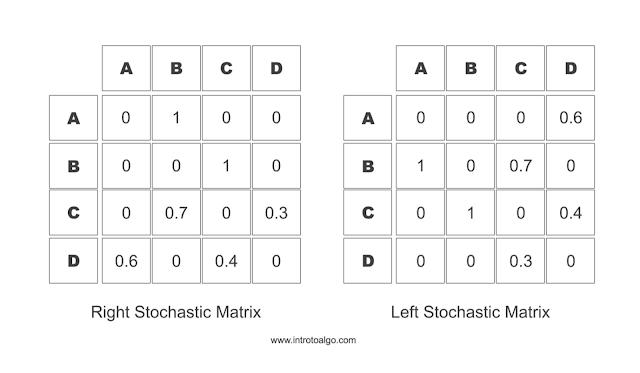
A Stochastic matrix or transition matrix is a matrix used to define the transitions in a Markov Chain. In a Stochastic matrix, each entry is a non negative real number which represents the probability of the state change from a to x, where a is the current state which is given as a row and x is the next possible state reachable from a, this type of stochastic matrix is also known as a right stochastic matrix in which the probability in each row sum's up to 1. Similarly, one can define the transition the other way around i.e. transition where column denotes the current state and the values in each row denotes the transition probability for the jump from current state, This type of transition matrix is coined as a left stochastic matrix. In left stochastic matrix, the probability in each column sums up to 1. These kind of matrix have various names such as probability matrix, transition matrix, stochastic matrix, Markov matrix or substitution matrix.

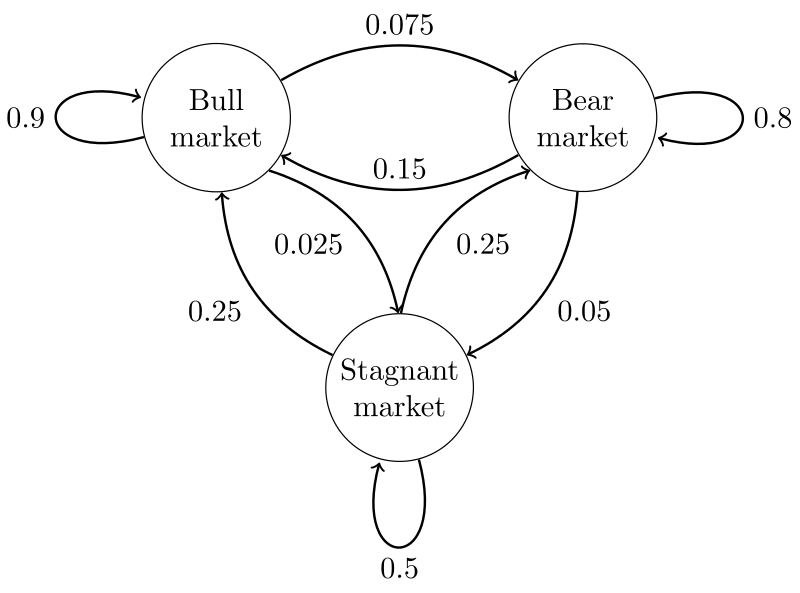
Code for modeling markov process as described in Fig 2.