Merge Sort
(Sorting Algorithm)

In this post we will learn about merge sort algorithm. Merge sort is an algorithm in which we apply divide and conquer strategy. i.e. we first divide the given sequence into several parts until we get the minimum easily solvable part and then we combine those parts to get a sorted sequence.

Let us check the Merge Sort algorithm and try to understand it line by line.

mergeSort( low , high )
{
if( low < high ) then:
mid = lowerBound( (low + high) / 2)
mergeSort( low , mid )
mergeSort(mid+1 , high )
merge( low , mid , high )
}
MergeSort algorithm goes as follows:

1. we first check that low and high of the list are not equal , as if both are equal we don't need to further divide it and we just simply return the number.
2. If we know that the low index is less than high index, we calculate mid which is lower bound of low+mid / 2.
3. We further recursively call merge sort on the remaining two halves, i.e (low, mid) and (mid+1,high).
4. After completion of the recursive calls, we need to merge both the parts again which we do by using merge function. Now let us look at how merge function operates.

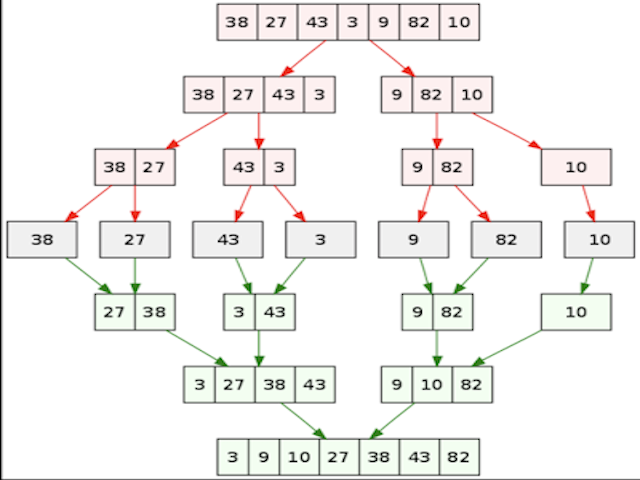
We will divide merge operation into 3 parts for easier understanding, Refer fig(a) for better understanding of what is happening in merge operation.

• PART 1 involves in Merging until one of the two part in array gets added to a temp array b.
• PART 2 involves in adding the remaining part to temp array b.
• PART 3 involves in recopying the elements of temp array b, back to a.

merge( low , mid , high )
{
j = low, k = mid+1, i = low;
// PART 1
while( j <= mid and k<=high )
{
if( a[j] < a[k] )
{
b[i] = a[j]
j++
}
else
{
b[i] = a[k]
k++
}
i++
}
// PART 1 ENDS HERE

// PART 2

if( j <= mid )
{
while( j <= mid )
{
b[i] = a[j]
j++ , i++
}
}
else
{
while( k <= high )
{
b[i] = a[k]
k++ , i++
}
}
//PART 2 ENDS HERE
//PART 3
i = low
while (i <= high )
{
a[i] = b[i]
i++
}
//PART 3 ENDS HERE
}

Fig.1 Shows the working of merge sort algorithm, First we are dividing the problem into subproblems and further dividing those subproblem into subproblems, until they become elementary, or their solution becomes obvious. In this case, we break until we get a single element as it is sorted in itself by its nature. After the process of division we further start to combine the obtained solution to the subproblems. In this case we apply merge algorithm to combine it.

Fig 2: Merge Sort: Merge Algorithm

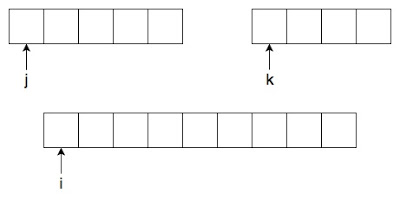
Now let us understand the Merge algorithm part by part, First thing you need to note is that the array to which i is pointing is a duplicate array which we are using for merge process. The array which is being pointed by j is the left subpart while the array which is pointed by k is the right subpart which we intend to merge. (Refer Merge Algorithm) & note that the list pointed by j and k will always be sorted as we are dividing until we get the subproblem which is sorted by nature (single element). and combining the sorted list will further give a sorted list.

PART 1: In part 1 of merge, we basically just compare value at j and value at k and move the smaller element to the position i until we complete the list pointed by j or list pointed by k, whichever happens first.

PART 2: continued after part 1, in part 2 if the list pointed by j is finished first, then it means there is some element left in the list pointed by k, so we move all the elements in k to the position pointed by i sequentially until it completes.

PART 3: part 3 involves of updating the original list, as the sorted and combined list of elements is in the duplicate list, pointed by i.

PROGRAM IN CPP