Minimum Spanning
Tree

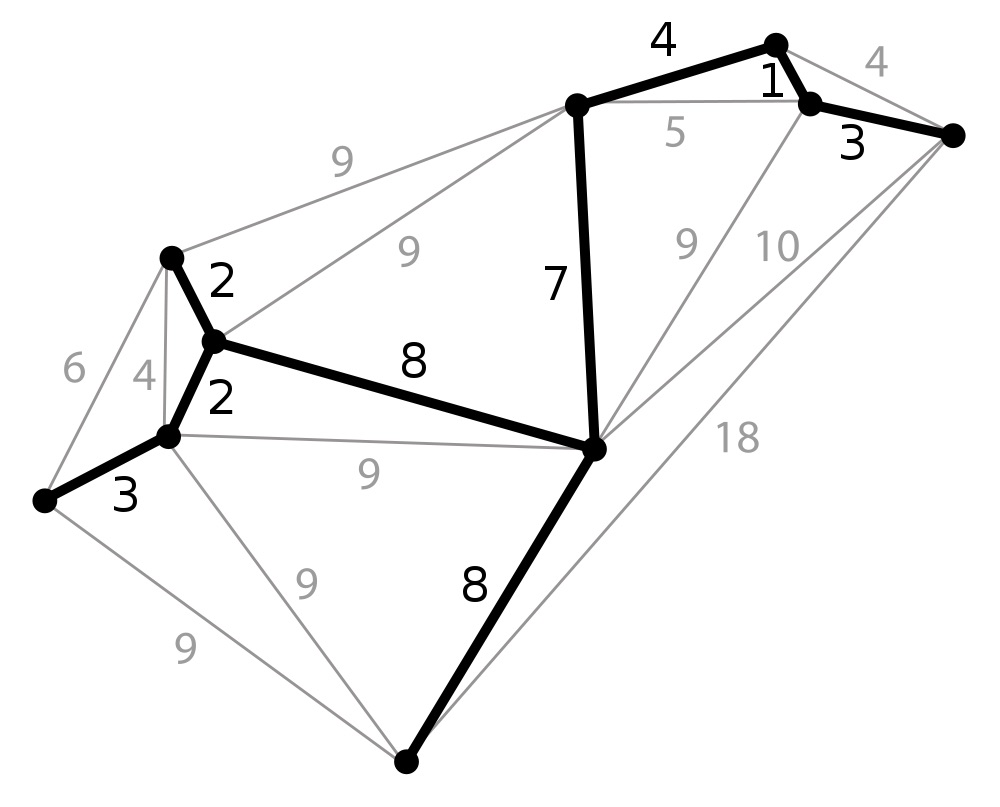
Let us deduce the problem of finding a minimum spanning tree from a given graph, for that we need to know how the tree is different from a graph and what minimum spanning tree actually is...

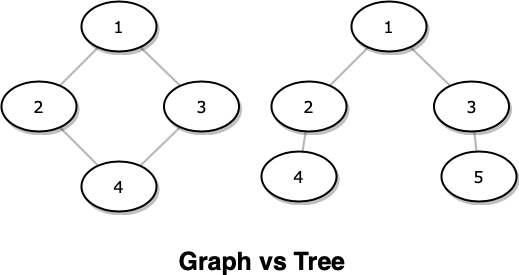
So let us go by the definition, A graph is set of nodes and edges whereas a tree is a set of nodes and vertices with no cycles, so the only thing in which a tree differs is on the fact that trees do not contain cycles.

If tree does not contain cycles, then it basically means that, we need to remove the cycles to convert a graph into a tree and so if we want a minimum spanning tree then we need to remove the edges forming a cycle with larger weight, i.e we only keep the edges with minimum weight , in the graph and keep including the edges which do not form a cycle, until all the edges are considered. So this method is basically Kruskals Method for finding Minimum Spanning Tree. Tap the below canvas to stimulate a minimum spanning tree.

So to find a minimum spanning tree, we have to follow some simple steps which are stated as follows:

That's it, after following these steps what remains is the minimum spanning tree, so now the only abstract thing in the description which remains is how do we check whether a cycle is formed if we include the edge.

The thing is, we solve the above problem by applying Union Find method, whose some of the good resources are :
1. Geek For Geeks ( Great for understanding how we detect cycles using Union Find Method )
2. William Fiset ( Great for understanding how union and find method works )

In union-find algorithm by using union method, we simply join two sets and by using find method we can find the root of the given set, its like we create small graphs or sets with a central element which can be found using find method and if we want to join two sets we can simply use the union method.

Suppose there are 5 nodes : 0, 1, 2, 3 and 4. and we want to perform the operations as follows:
1. union(0,1)
2. union(2,3)
3. union(3,1)
4. union(2,4)

Initially :
0 1 2 3 4
-1 -1 -1 -1 -1

after union(0,1)
0 1 2 3 4
1 -1 -1 -1 -1

after union(2,3)
0 1 2 3 4
1 -1 -1 2 -1

after union(3,1)
0 1 2 3 4
1 3 -1 2 -1

after union(2,4)
0 1 2 3 4
1 3 -1 2 2

So after looking at the above example, we can see what's happening and how different disjoint sets are getting merged into one by the use of union function, and at each stage we can also see what actually is the output of the find function so, now using union and find we can devise a simple but effective algorithm for finding whether a given graph contains a cycle, So for that we first create an empty union structure for N nodes in the graph (like in a). After that we pick an edge as in step two of the Kruskal's algorithm and then we see the start and end vertices of the edge and check if they find returns different values (same is allowed only if it is -1 i.e Self-loop) which tells that they are disjoint so no cycle is formed after inclusion of the edge but if the condition is not true, then we know that after including the edge, it will add a cycle in the tree so we simply discard the edge.

lets see the code for calculating a minimum spanning tree from the given graph